Equations

Equations and graphs

Consider this table of values of $x$ and $y$ .

$x$	$y$
0	20
1	30
2	40
3	50

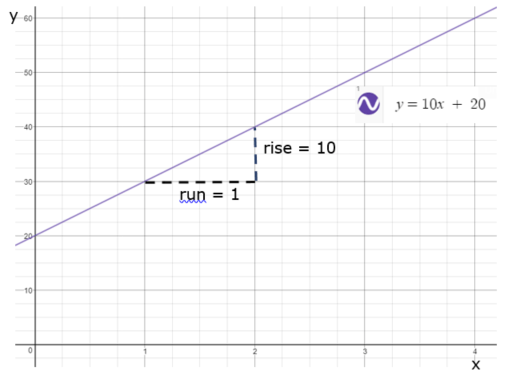
Notice that for every increase of $1$ in the $x$ the $y$ increases by $10$ . This constant difference shows that there is a linear relationship between $x$ and $y$ . If we plot the values on the axes we get the straight line in the graph above.

Gradient

The gradient of the line is $10$ . The gradient of any line can be calculated using the formula rise over run (either by reading off the graph or using any two coordinates from the table).

$gradient = m =$ $\frac{rise}{run}$ $=$ $\frac{y_2 - y_1}{ x_2 - x_1}$

e.g. Point 1: $(x_1,y_1) =$ $(1,30)$ and Point 2: $(x_1,y_1) =$ $(3,50)$

$gradient = m =$ $\frac{50 - 30}{3 - 1}$ $=$ $\frac{20}{ 2}$ $= 10$

Straight line equations

The general form of a straight line is $y = mx + c$

Where $m$ is the gradient of the line and $c$ is the $y$ intercept (i.e. where the line crosses the $y$ axis).
This form is handy for sketching a line and for reading off the gradient.

e.g. Sketch the line $y = -\frac{1}{2}x + 10$

The $gradient =$ $-\frac{1}{2}$ and the $y$ $intercept = 10$

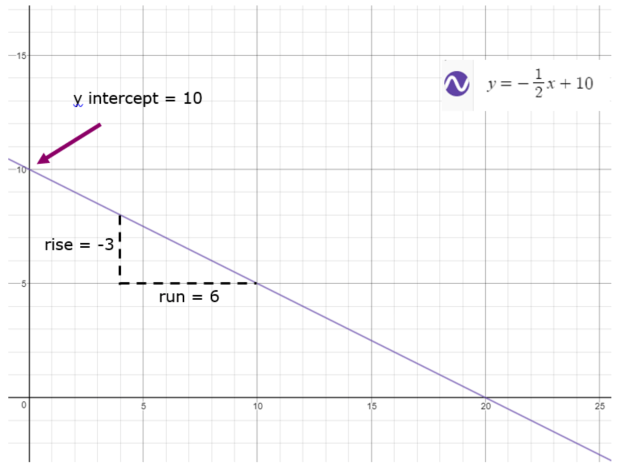
Note that sometimes we need to rearrange an equation into the form $y = mx + c$ .

e.g. Find the gradient and y intercept of the line $2y - 6x = 4$

$2y = 4 + 6x$

$y = 2 + 3x$

The line will cut the $y$ axis at $2$ with a gradient of $3$ .

Use the desmos online calculator to draw different straight lines to understand the relationship between the equation and the graph.

Special graphs

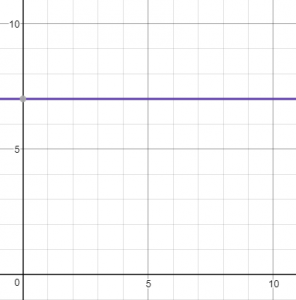
Horizontal lines

Line: $y= 7$

Gradient = 0

Vertical Lines

Line: $x=6$

Gradient = undefined

Parallel Lines

Lines: $y=x+4$ and $y=x+1$

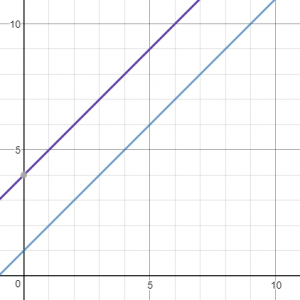
The gradient of parallel lines are equal.

Tables and graphs drag and drop activity

Complete the following interactive activity

Further information

Press the Printer Friendly button at the top left-hand corner to download a printable handout
Khan academy uses video to explain another worked example of drawing a line with slope and intercept and a set of practice problems that you can use to review your understanding.

Learning Hub

Learning Hub team
Workshops
Drop in booth
Learning leaders
Pass Leaders
Business library guides

Life on campus
Careers centre
Student support
He Tuākana
AskAuckland student centre