Simultaneous equations

In Economics we are interested in the point where the Supply and Demand curves intersect (the point of equilibrium). We can read the coordinate of the intersection off the graph or use simultaneous equations.

Using a Graph

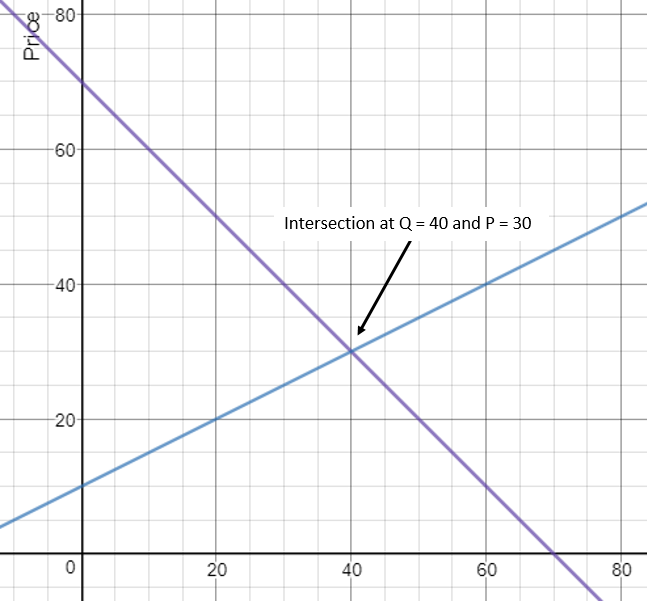
For example:

Supply curve:  

Demand curve: 

The intersection (equilibrium) is at Price = 30 and Quantity = 40.

Simultaneous equations

We use the rules of rearranging equations to solve the two equations simultaneously.

For example:

Supply curve:  

Demand curve: 

Step 1

Make the equations equal to each other

Step 2

Rearrange the equation by moving all Qs to the same side and any numbers to the other side to give the value of Q

   (add Q to both sides to move it to the left of the equal sign)

   (subtract from both sides to move the to the right of the equal sign)

   (divide both sides by to give the value of )

Step 3

Substitute the value of Q into one of the initial equations to find the value of P.

To find P substitute Q = 40 into one of the initial equations.

  (substitute Q = 40 into the Demand equation)

Notice that we have the same solution as before (Price = 30, Quantity = 40)

Further example:

The following  video will take you through another example of solving simultaneous equations.

Further information

• Press the Printer Friendly button at the top left-hand corner to download a printable handout
• Khan academy use video to explain another  worked example where the equations are rearranged differently and a set of  practice problems that you can use to review your understanding.