Percentages
A percentage (%) is a number expressed as a part of 100. Percentages can be converted to decimals and fractions. Below are some common calculations that use percentages.
Expand the following boxes for information on how to solve common percentage problems. Each problem type has a video of a worked problem.
Percentage of an amount
Many percentage calculations can be done in your head. For example, 50% of 200. Since 50% is the same as or a half (
) we can find a half of 200 to get 100.
Other calculations can be completed on your calculator.
Step 1: change the percentage to a decimal.
Step 2: multiply this decimal by the number you want to find the percentage of.
e.g. To find % of
, enter the calculation
into your calculator:
.
For further explanations of finding a percentage of an amount see Khan academy.
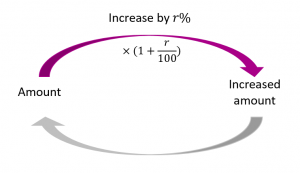
Increase by a percentage
The best way to increase an amount by a percentage is to use a one-step method.
To increase an amount by 25% we multiply by 1.25. The 1 represents the whole amount and the 0.25 represents the additional 25%.
e.g. The widget share value has increased from $2.85 by 16%. Find the new share value:
$2.85 x 1.16 = $3.306 = $3.31 (rounded to 2 decimal places).
For a further explanation of increasing by a percentage see Khan academy.
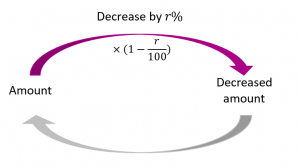
Decrease by a percentage
Decreasing the value of a quantity by a percentage is also best done with a one-step method.
Think about what percentage of the quantity is left after the percentage decrease.
For example, a decrease of 20% will leave 80% of the quantity. Therefore, to find the decreased amount we multiply by 1 minus the percentage decrease (expressed as a decimal).
For example, my car’s value has decreased from $11,500 by 5%. Find the new value of the car:
$11,500 x 0.95 = $10,925.
Further information
- Khan academy has online videos to explain many aspects of calculating with percentages. Khan academy.